学习与记录。

0%

堆排序中建立初始大根堆的时间复杂度分析

发表于 更新于 分类于 Valine：

本文主要记录对堆排序中建立初始大根堆部分的时间复杂度的分析。结论为 O(n)。

代码

代码主要分为两部分，堆排序的主方法以及调整堆的方法，此处的堆为大根堆，对应升序排序。

堆排序主方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static void HeapSort(int[] nums)
{
    // 建立初始大根堆，时间复杂度 O(n)
    for (int i = nums.Length / 2 - 1; i >= 0; i--) {
        HeapAdjust(nums, i, nums.Length - 1);
    }
    // 依次确定最大值，与堆中的最后值交换，然后调整交换后的堆（不包括确定的值）
    for (int i = nums.Length - 1; i >= 0; i--) {
        int tmp = nums[0];
        nums[0] = nums[i];
        nums[i] = tmp;
        HeapAdjust(nums, 0, i - 1);
    }
}

调整堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private static void HeapAdjust(int[] nums, int root, int end)
{
    // 待调整值
    int value = nums[root];
    // child 为子元素的下标
    for (int child = root * 2 + 1; child < end; child = child * 2 + 1) {
        // 取父元素左右子树中的最大值
        if (child < end - 1 && nums[child] < nums[child + 1]) {
            ++child;
        }
        // 待调整值 >= 其左右子树中的最大值则 break
        if (value >= nums[child]) {
            break;
        }
        // 将子元素上升，然后更新根的下标
        nums[root] = nums[child];
        root = child;
    }
    // 将待调整值放入最终确定的位置
    nums[root] = value;
}

分析及证明

直接看代码的话可能会得出建立初始大根堆的时间复杂度为 O(nlogn) 的结论。

主方法中是一个 n/2 次的循环，调整堆的方法是一个 logn 次的循环，相乘确实是 O(nlogn) 没错。

事实上，每个节点并没有进行那么多次的调整。

接下来进行证明：（PS：以下的证明中，树的高度基数为 0，即叶子节点的高度为 0）

前提：建立初始大根堆的顺序是自下而上的。

  1. 首先，有一棵完全二叉树，具有 n 个元素，那么树的高度 h = logn。

  2. 调整堆是从这棵树的最后一个非叶子节点开始的，而该节点所在的层的高度为 1，因此该层节点只需要向下进行 1 次运算就能调整完成。

  3. 在调整上层元素时，不需要和下层的所有元素进行比较，只需要和其中之一的分叉进行比较即可，比较次数即为节点所在层的高度，因此，第 i 层的元素的计算量为 2^(h - i) * i。

  4. 由以上的通项公式可以得知，建立初始大根堆的精确时间复杂度为：

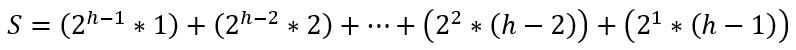
    formula00

  5. 该求和公式为等比数列与等差数列的乘积，因此可以使用错位相减法求解：

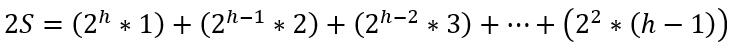
    formula01

  6. 用 2S 减去 S 得：

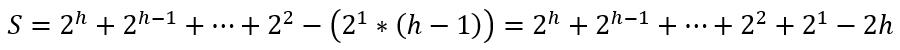
    formula02

  7. 由等比数列求和公式可得：

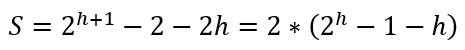
    formula03

  8. 将 h = logn 带入 S 中得：

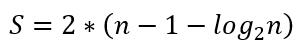
    formula04

因此，可以得出结论：建立初始大根堆的时间复杂度为 O(n)。