学习与记录。

0%

红黑树插入删除后的修正操作详解

发表于 更新于 分类于 Valine：

本文主要记录红黑树插入删除后的修正操作详解，以及对应的实现（C#）。

红黑树的规则

首先明确一下红黑树的规则：

  1. 每个节点不是红色就是黑色；
  2. 根节点一定为黑色；
  3. 如果节点为红色，其子节点一定为黑色；
    1. 红黑树的任何一条路径上不存在连续的两个红色节点。
  4. 叶子节点一定为黑色（此处的叶子节点指无值节点 NIL）；
  5. 从根节点到叶节点的每条路径，必须包含相同数目的黑色节点。
    1. 红黑树的最长路径长度最多为最短路径长度的两倍，最长路径黑红节点交替，最短路径节点全黑。

插入修正

设祖父节点为 grand，父节点为 parent，叔叔节点为 uncle，插入的节点为 node。

关于红黑树的插入操作，node 的颜色选择：

  1. node 默认为黑色的话，那么 node 插入后一定会增加某条路径上的黑色节点数量，因此每一次的插入都需要进行修正；
  2. node 默认为红色的话，只有当 parent 为红色时，才会违反红黑树的规则，才需要进行修正。

所以 node 默认为红色。

接下来再看插入后的修正操作：

因为红黑树以黑色节点的数量来维持平衡，所以：

  1. 当 parent 为黑色时，node 插入后，各路径的黑色节点数量不变，因此不会对红黑树的平衡产生影响，不需要进行修正；
  2. 当 parent 为红色时，因为红色节点的两个子节点只能为黑色节点，而 node 默认为红色，因此会违反红黑树的规则，需要进行修正。

另外，关于 uncle 的说明：

如果 uncle 为黑色，那么 uncle 一定为 NIL 节点，因为 parent 为红色，所以有两个黑色子树，而 node 既然能插入到 parent 下方，说明 parent 最多存在一个有值子树，而只有一个子树的话，很明显两条子树的路径是不平衡的，所以 parent 的两个黑色子树一定均为 NIL 节点。因此，uncle 如果为黑色，那么一定为 NIL 节点。

进行修正的条件：

1
2
3
4
5
6
private void AddFixedUp(Node node)
{
    while (Node.IsRed(node.Parent)) {
        // ...
    }
}

（注：以下是 parent 为 grand 的左子树的情况，当 parent 为 grand 的右子树时，执行镜像操作即可。）

Case 1：uncle 为红色

将 uncle 和 parent 置黑，grand 置红，然后把 grand 当作插入节点，再进行一次修正。

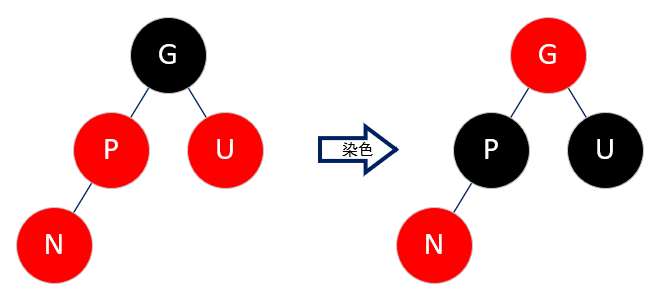
insert-case-1

这样相当于将 grand 的黑色下沉到了 parent 和 uncle，所以各路径的黑色节点数量保持不变，不会影响树的平衡。

但是由于 grand 置红了，可能导致 grand 与 grand’s parent 产生冲突，所以要把 grand 当作插入节点，再进行一次修正。

1
2
3
4
parent.Color = uncle.Color = Node.BLACK;
grand.Color = Node.RED;
node = grand;
continue;

当 grand 刚好为 root 时，root 为红色是违反规则的，所以在全部修正结束后，需要将 root 置黑，以保证不违反红黑树的规则。

1
Root.Color = Node.BLACK;

Case 2：uncle 为黑色，且 node 为 parent 的右子树

将 parent 左旋，然后把 node 当作 parent，parent 当作 node。（图中的交换是交换引用的对象，不是交换值）

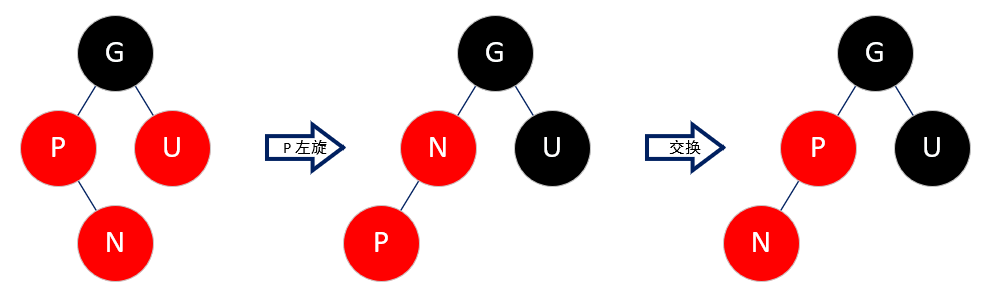
insert-case-2

这样的目的是将 Case 2 转换为 Case 3。

1
2
3
4
LeftRotate(parent);
Node tmp = parent;
parent = node;
node = tmp;

Case 3：uncle 为黑色，且 node 为 parent 的左子树

将 parent 置黑，grand 置红，然后将 grand 右旋。

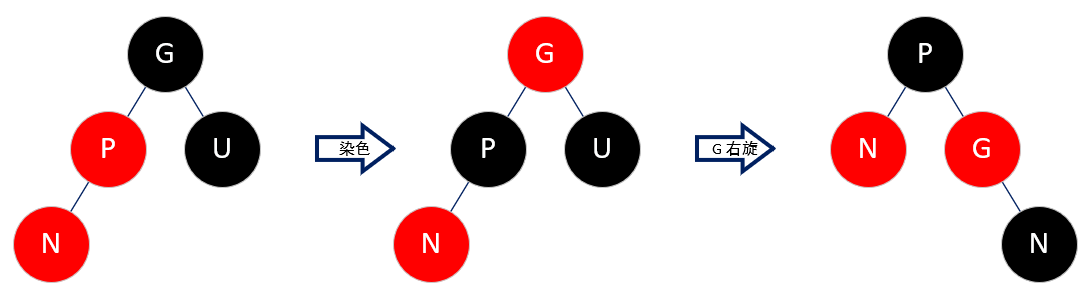
insert-case-3

grand 右旋后，parent 就到了原先 grand 的位置，为了黑色节点的数量保持不变，便将 parent 置黑，grand 置红，这样左分支和右分支的黑色节点数量不变，不会影响树的平衡。

1
2
3
parent.Color = Node.BLACK;
grand.Color = Node.RED;
RightRotate(grand);

完整代码

包括 parent 为 grand 左子树和右子树的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
private void AddFixedUp(Node node)
{
    // node.Parent 为红色
    while (Node.IsRed(node.Parent)) {
        Node parent = node.Parent, grand = parent.Parent;
        if (parent == grand.Left) {
            // parent 为 grand 左子树
            Node uncle = grand.Right;
            // Case 1: uncle 为红色
            if (Node.IsRed(uncle)) {
                parent.Color = uncle.Color = Node.BLACK;
                grand.Color = Node.RED;
                node = grand;
                continue;
            }
            // Case 2: uncle 为黑色，且 node 为 parent 的右子树（转换为 Case 3）
            if (node == parent.Right) {
                LeftRotate(parent);
                Node tmp = parent;
                parent = node;
                node = tmp;
            }
            // Case 3: uncle 为黑色，且 node 为 parent 的左子树
            parent.Color = Node.BLACK;
            grand.Color = Node.RED;
            RightRotate(grand);
        } else {
            // parent 为 grand 右子树
            Node uncle = grand.Left;
            // Case 1: uncle 为红色
            if (Node.IsRed(uncle)) {
                uncle.Color = Node.BLACK;
                parent.Color = Node.BLACK;
                grand.Color = Node.RED;
                node = grand;
                continue;
            }
            // Case 2: uncle 为黑色，且 node 为 parent 的左子树（转换为 Case 3）
            if (node == parent.Left) {
                RightRotate(parent);
                Node tmp = parent;
                parent = node;
                node = tmp;
            }
            // Case 3: uncle 为黑色，且 node 为 parent 的右子树
            parent.Color = Node.BLACK;
            grand.Color = Node.RED;
            LeftRotate(grand);
        }
    }
    // 将 root 置黑
    Root.Color = Node.BLACK;
}

删除修正

设父节点为 parent，兄弟节点为 sibling，待删除的节点为 delete，替代节点为 node。

关于二叉搜索树的删除操作，根据 delete 的子树情况分为三种情况：

  1. 没有任何子树，那么 node 就是 NIL 节点，可以直接删除 delete；
  2. 存在一个子树，那么 node 就是这个子树，删除 delete，用 node 替代 delete；
  3. 存在两个子树，那么找到 delete 在中序遍历下的后继节点 successor，修改 delete 的值为 successor 的值，然后把 successor 当作 delete 再执行一次删除操作。

由此可知，最终被删除的节点一定不同时存在左右子树。

（注：之后的内容中的 delete 均指最终被删除的节点。）

接下来再看删除后的修正操作：

因为红黑树以黑色节点的数量来维持平衡，所以：

  1. 当 delete 为红色时，删除后不会对红黑树的平衡产生影响。
    1. 因为红色节点的子树都是黑色节点，如果 delete 只存在一个子树的话，会导致子树的两条路径不平衡，所以此时 delete 的子树一定都是 NIL 节点。
  2. 当 delete 为黑色时，该节点所在路径的黑色节点数量会减少，因此会导致不平衡，需要进行修正。
1
2
3
if (Node.IsBlack(delete)) {
    RemoveFixedUp(node, delete.Parent);
}

在删除黑色 delete 后，根据 node 的颜色进行修正：

  1. node 为红色时，直接置黑就可以补充被删除的黑色；
  2. node 为黑色时，则需要分情况讨论。

另外，关于 sibling 的说明：

sibling 一定不为 NIL 节点，因为 delete 为黑色且不为 NIL 节点，所以 delete 及之后的路径至少包含两个黑色节点（包括 delete 自身和 NIL 叶子节点），如果 sibling 为 NIL 节点的话，那么 sibling 及之后的路径只有 sibling 一个黑色节点，这样的话 parent 的左右子树路径就是不平衡的，这在一颗符合规则的红黑树中是不存在的，所以 sibling 一定不为 NIL 节点。

进行修正的条件：

1
2
3
4
5
6
private void RemoveFixedUp(Node node, Node parent)
{
    while (Node.IsBlack(node) && node != Root) {
        // ...
    }
}

（注：以下是 node 为 parent 的左子树的情况，当 node 为 parent 的右子树时，执行镜像操作即可。）

Case 1：sibling 为红色

因为 sibling 为红色，所以 parent 一定为黑色，所以将 parent 置红，sibling 置黑，再将 parent 左旋。

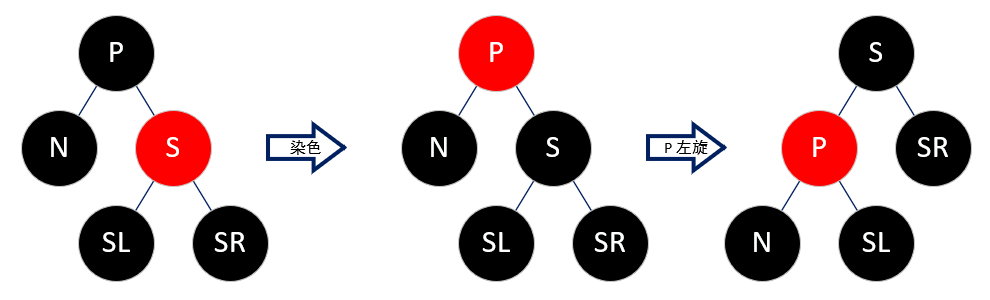
delete-case-1

这样相当于将右路的红色节点转到了左路，不会影响树的平衡。

修正后，黑色的 sibling.left 成了新的 sibling，这样就将 Case 1 转换为了 Case 2 或 Case 3 或 Case 4。

1
2
3
4
parent.Color = Node.RED;
sibling.Color = Node.BLACK;
LeftRotate(parent);
sibling = parent.Right; // new sibling

Case 2：sibling 为黑色，且 sibling 的左右子树均为黑色

将 sibling 置红，然后把 parent 当作 node，再进行一次修正。（粉色表示任意颜色均可）

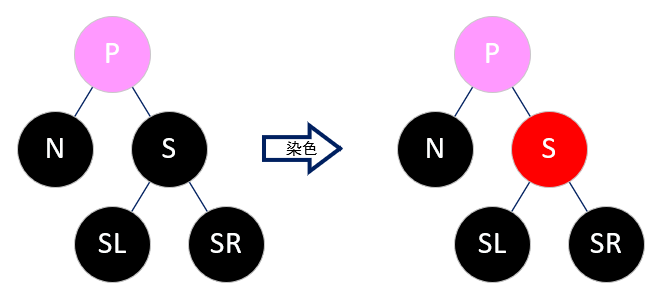
delete-case-2

因为删除节点后，左路少了一个黑，而右路的 sibling 及其左右子树均为黑色，所以可以直接将 sibling 置红，这样右路也少了一个黑，左右路就平衡了。

与此同时，经过 parent 这个节点的所有路径就整体少了一个黑，所以接下来就需要处理 parent 路径和其他路径的平衡，也就是把 parent 当作 node，再进行一次修正。

1
2
3
4
sibling.Color = Node.RED;
node = parent;
parent = node.Parent;
continue;

sibling 被置红，但是 parent 的颜色是不确定的，如果 parent 是红色就会导致连续出现红色节点的情况，而且 node = parent 后进行的新一次修正，是不符合修正条件的，会直接结束，所以在修正循环结束后，需要手动将 node（也就是 parent）置黑。

1
2
3
if (node != null) {
    node.Color = Node.BLACK;
}

Case 3：sibling 为黑色，且 sibling 的左子树为红色，右子树为黑色

将 sibling 置红，sibling.left 置黑，然后将 sibling 右旋。

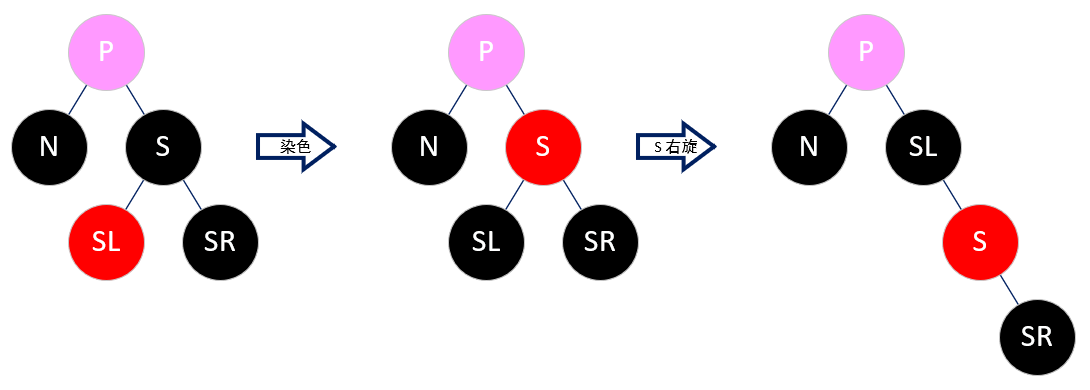
delete-case-3

这样相当于把 sibling 左路的红色转到 sibling 的右路，不会影响树的平衡。

修正后，黑色的 sibling.left 就成了新的 sibling，而新的 sibling.right 为红色，这样就将 Case 3 转换为了 Case 4。

1
2
3
4
sibling.Left.Color = Node.BLACK;
sibling.Color = Node.RED;
RightRotate(sibling);
sibling = parent.Right;

Case 4：sibling 为黑色，且 sibling 的左子树为任意色，右子树为红色

将 sibling 置为 parent 的颜色，然后将 parent 和 sibling.right 置黑，再将 parent 左旋。

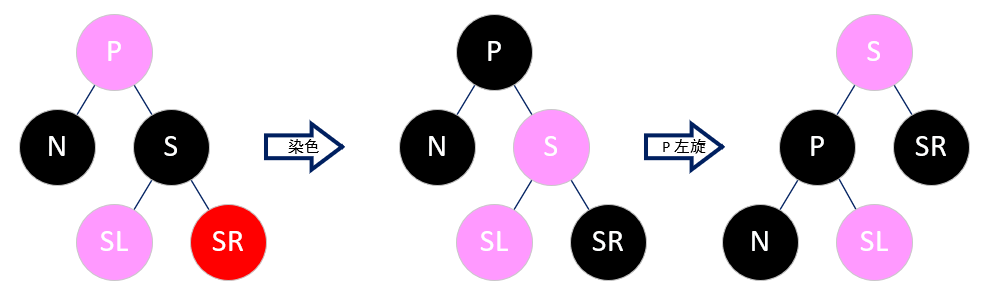
delete-case-4.jpg

左旋后，sibling 就到了原先 parent 的位置，为了黑色节点数量保持不变，所以将 sibling 置为 parent 的颜色。但 sibling 换位并变色会导致右路少了一个黑色节点，所以将 sibling.right 置黑以保持平衡。最后将 parent 置黑，这样左路因删除节点而缺少的一个黑色节点，由 parent 进行了补充，整棵红黑树就平衡了。

1
2
3
4
sibling.Color = parent.Color;
parent.Color = Node.BLACK;
sibling.Right.Color = Node.BLACK;
LeftRotate(parent);

完整代码

包括 node 为 parent 左子树和右子树的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
private void RemoveFixedUp(Node node, Node parent)
{
    // node 为黑色且不为根节点
    while (Node.IsBlack(node) && node != Root) {
        if (node == parent.Left) {
            // node 为 parent 左子树的情况
            Node sibling = parent.Right;
            // Case 1: sibling 为红色（转换为 Case 2, 3, 4）
            if (Node.IsRed(sibling)) {
                parent.Color = Node.RED;
                sibling.Color = Node.BLACK;
                LeftRotate(parent);
                sibling = parent.Right; // new sibling
            }
            // Case 2: sibling 为黑色，且 sibling 的左右子树都为黑色
            if (Node.IsBlack(sibling.Left) && Node.IsBlack(sibling.Right)) {
                sibling.Color = Node.RED;
                node = parent;
                parent = node.Parent;
                continue;
            }
            // Case 3: sibling 为黑色，且 sibling 的左子树为红色，右子树为黑色（转换为 Case 4）
            if (Node.IsRed(sibling.Left)) {
                sibling.Left.Color = Node.BLACK;
                sibling.Color = Node.RED;
                RightRotate(sibling);
                sibling = parent.Right;
            }
            // Case 4: sibling 为黑色，且 sibling 的左子树为任意色，右子树为红色
            sibling.Color = parent.Color;
            parent.Color = Node.BLACK;
            sibling.Right.Color = Node.BLACK;
            LeftRotate(parent);
            break;
        } else {
            // node 为 parent 右子树的情况
            Node sibling = parent.Left;
            // Case 1: sibling 为红色（转换为 Case 2, 3, 4）
            if (Node.IsRed(sibling)) {
                parent.Color = Node.RED;
                sibling.Color = Node.BLACK;
                RightRotate(parent);
                sibling = parent.Left; // new sibling
            }
            // Case 2: sibling 为黑色，且 sibling 的左右子树都为黑色
            if (Node.IsBlack(sibling.Left) && Node.IsBlack(sibling.Right)) {
                sibling.Color = Node.RED;
                node = parent;
                parent = node.Parent;
                continue;
            }
            // Case 3: sibling 为黑色，且 sibling 的左子树为黑色，右子树为红色（转换为 Case 4）
            if (Node.IsRed(sibling.Right)) {
                sibling.Right.Color = Node.BLACK;
                sibling.Color = Node.RED;
                LeftRotate(sibling);
                sibling = parent.Left;
            }
            // Case 4: sibling 为黑色，且 sibling 的左子树为红色，右子树为任意色
            sibling.Color = parent.Color;
            parent.Color = Node.BLACK;
            sibling.Left.Color = Node.BLACK;
            RightRotate(parent);
            break;
        }
    }
    if (node != null) {
        node.Color = Node.BLACK;
    }
}